I. ĐẠI SỐ

1) Định nghĩa, tính chất căn bậc hai

a) Với số dương a, số \( \sqrt{a} \) được gọi là căn bậc hai số học của a.

b) Với a ≥ 0 ta có \( x = \sqrt{a} \Leftrightarrow  \left\{\begin{matrix} x ≥0  \\ x^2 = (\sqrt{a})^2 = a    \end{matrix}\right. \)

c) Với hai số a và b không âm, ta có: \( a < b\Leftrightarrow  \sqrt{a} < \sqrt{b} \)

d)  \( \sqrt{A^2} = |A|= \left [ \begin{matrix}  A; A ≥ 0 \\ -A ; A < 0    \end{matrix}\right. \)

2) Các công thức biến đổi căn thức

1.    \( \sqrt{A^2} = |A| \)             

2.    \( \sqrt{AB} = \sqrt{A}.\sqrt{B} \) (A ≥ 0, B ≥ 0)

3.    \( \left ( \cfrac{A }{B }  \right ) = \cfrac{\sqrt{A} }{\sqrt{B} } \) , ( A ≥ 0, B > 0 )       

4.    \( \sqrt{A^2 B} = |A | \sqrt{B}  \)

5.    \( A \sqrt{B} = \sqrt{A^2 B } \), ( A ≥ 0; B ≥ 0 )

\( A \sqrt{B} =-  \sqrt{A^2 B } \), ( A < 0; B ≥ 0 )

6.    \( \sqrt{ \cfrac{A }{ B} } = \cfrac{ 1}{|B| } \sqrt{AB}   \) , ( AB ≥ 0 , B ≠ 0 )

7.    \( \cfrac{ C}{ \sqrt{A} ± B } = \cfrac{C \left ( \sqrt{A} \mp B  \right )  }{ A - B^2 }  \) \( ( A ≥ 0 , A ≠ B^2 ) \)

8.    \( \cfrac{A }{ \sqrt{B} } = \cfrac{ A \sqrt{B}}{ B} \)  , ( B > 0 )        

9.    \( \cfrac{ C}{ \sqrt{A} ± \sqrt{B} } = \cfrac{C (\sqrt{A} \mp \sqrt{B })  }{A - B  } \), ( A,B ≥ 0 , A ≠ B )

3) Định nghĩa, tính chất hàm số bậc nhất

a) Hàm số bậc nhất là hàm số được cho bởi công thức \( y = ax + b \)  ( \( a, b\in  R\)  và a ≠ 0)

b) Hàm số bậc nhất xác định với mọi giá trị  \( x \in R\).

     Hàm số đồng biến trên R khi a > 0. Nghịch biến trên R khi a < 0.

4) Đồ thị của hàm số \( y = ax + b \) (a ≠  0) là một đường thẳng cắt trục tung tại điểm có tung độ bằng b (a: hệ số góc, b: tung độ gốc) và cắt trục hoành tại điểm có hoành độ bằng \( \cfrac{ -b}{a } \).

5) Cho \( (d): y = ax + b\)  và \(  (d'): y = a'x + b'\)  (a, a’ ≠ 0). Ta có:

\( (d) \equiv   (d') \Leftrightarrow  \left\{\begin{matrix}  a = a'  \\  b = b'   \end{matrix}\right. \)        

\( (d) //  (d') \Leftrightarrow  \left\{\begin{matrix}  a = a'  \\  b ≠ b'   \end{matrix}\right.\)

\( (d) \cap  (d') \Leftrightarrow   a ≠   a'   \)

\( (d) \perp    (d') \Leftrightarrow    a . a' = 1  \)

6) Gọi  α là góc tạo bởi đường thẳng y = ax + b và trục Ox thì:

        Khi a > 0 ta có \( \tan α = a \)

        Khi a < 0 ta có \( \tan α’ = |α| \)   ( α’ là góc kề bù với góc α )

II. HÌNH HỌC

1) Các hệ thức về cạnh và đường cao trong tam giác vuông.

       Cho ΔABC vuông tại A, đường cao AH. Ta có:

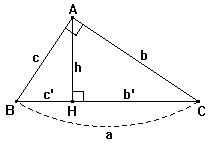
1) \( b^ 2  = a.b’ \)

    \( c^2 = a.c’ \)          

2) \( h^2 = b’. c’ \)

3) \( a.h = b.c \)

4) \( \cfrac{ 1}{h^2 } = \cfrac{ 1}{ b^2} + \cfrac{1 }{ c^2} \)

5) \( a^2 = b^2 + c^2\)  (Định lí Pytago)

2) Tỉ số lượng giác của góc nhọn

a) Định nghĩa các tỉ số lượng giác của góc nhọn 

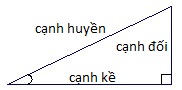
\( \sin α = \cfrac{ cạnh \: đối }{ cạnh \: huyền } \)

\( \cos α = \cfrac{cạnh \: kề  }{cạnh \: huyền  } \)

\( \tan α = \cfrac{ cạnh \: đối }{ cạnh \: kề } \)

\( \cot α = \cfrac{ cạnh \: kề }{ cạnh \: đối } \)

b) Một số tính chất của các tỉ số lượng giác

+ Cho hai góc α và β phụ nhau. Khi đó:

    \( \sin α = \cos β \)               \(  \cos α = \sin β \)  

    \( \tan α = \cot β \)                 \( \cot α = \tan β \)

+ Cho góc nhọn α. Ta có:

\( 0 < \sin α < 1 \)                \( 0 < \cos α < 1 \)

\( \tan α = \cfrac{ \sin α}{\cos α } \)     

\( \cot α  = \cfrac{\cos α  }{ \sin α }  \)

\(  \sin^2 α + \cos^2α  = 1  \)

\(   \tan α. \cot α = 1 \)

c) Các hệ thức về cạnh và góc trong tam giác vuông: Định lí SGK/ 86

3) Các định lí trong đường tròn

a) Định lí về đường kính và dây cung

    + Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

    + Đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.

b) Các tính chất của tiếp tuyến

    + Nếu một đường thẳng là một tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

    + Nếu một đường thẳng vuông góc với bán kính tại một điểm nằm trên đường tròn thì đường thẳng đó là một tiếp tuyến của đường tròn.

    + Nếu 2 tiếp tuyến của một  đường tròn cắt nhau tại một điểm thì:

- Điểm đó cách đều hai tiếp điểm.

- Đường thẳng đi qua điểm đó và tâm đường tròn là đường phân giác của góc hợp bởi hai tiếp tuyến và góc hợp bởi hai bán kính,đồng thời là đường trung trực của dây nối hai tiếp điểm.

c) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.

     Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.

d) Định lí liên hệ giữa dây và khoảng cách đến tâm:  SGK/ 105 

e) Vị trí tương đối của đường thẳng và đường tròn: SGK/ 109

g) Vị trí tương đối của hai đường tròn: SGK/ 121