a) Hướng dẫn: dùng công thức tính Δ để tìm nghiệm phương trình bậc hai \( x^2 + 3x -10 = 0 \)

\( Δ = 3^2 -4.1.(-10)= 49 \)

Do Δ > 0 nên phương trình đã cho có 2 nghiệm phân biệt:

\( \left [ \begin{matrix} x_1 = \cfrac{-3+\sqrt{49} }{2 }= 2   \\  x_2 = \cfrac{-3-\sqrt{49} }{2 }= -5    \end{matrix}\right. \)

b\( \left\{\begin{matrix} x+3y = 6 \\ x - 2y =1    \end{matrix}\right. \)

\( \Leftrightarrow  \left\{\begin{matrix} x = 6-3y  \\ x - 2y =1    \end{matrix}\right. \)

\( \Leftrightarrow  \left\{\begin{matrix} x = 6-3y  \\ 6-3y - 2y =1    \end{matrix}\right. \)

\( \Leftrightarrow  \left\{\begin{matrix} x = 6-3y  \\ -5y  =-5   \end{matrix}\right. \)

\( \Leftrightarrow  \left\{\begin{matrix} x = 6-3.1=3  \\ y  =1   \end{matrix}\right. \)

Vậy hệ phương trình đã cho có 1 cặp nghiệm \( \left\{\begin{matrix} x = 3  \\ y  =1   \end{matrix}\right. \)

a) 

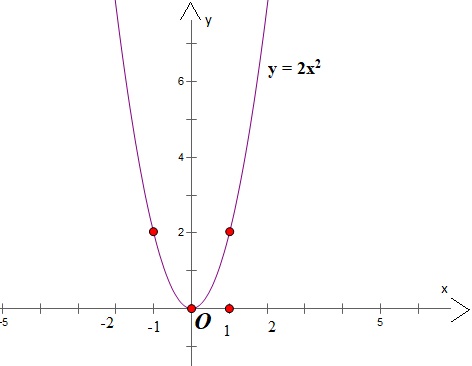
b) Phương trình hoành độ giao điểm của (d) và (P):

\( 2x^2 = mx-2 \)

\( \Leftrightarrow  2x^2 -mx +2 = 0 \) (*)

Đường thẳng (d) tiếp xúc với parabol (P) khi phương trình (*) có nghiệm kép

\( => Δ = 0 \)

\( \Leftrightarrow  m^2 - 4.2.2 = 0 \)

\( \Leftrightarrow  m^2 = 16\)

\( \Leftrightarrow  m = \left [ \begin{matrix}  m = 4 \\   m= -4  \end{matrix}\right. \)

Vậy khi m = 4 hoặc m = - 4 thì đường thẳng (d) tiếp xúc với parabol (P).

Gọi x (m) là chiều rộng của mảnh đất ( x > 0 )

Chiều dài của mảnh đất là 2x+9 (m)

Theo bài toán, ta có diện tích của mảnh đất hình chữ nhật là \( 200m^2 \) nên ta có:

\( x.( 2x+9) = 200 \)

\( \Leftrightarrow  2x^2 +9x - 200 = 0 \)

\( \Leftrightarrow  \left [ \begin{matrix} x_1 = 8  \\  x_2  = \cfrac{-25 }{ 2} \: ( loại ) \end{matrix}\right. \)

Vậy chiều rộng của mảnh đất bằng 8m, chiều dài của mảnh đất bằng 25m ( 2.8+9 = 25 )

Chu vi của mảnh đất: \( 2.(8+25) = 66m \)