|
CHƯƠNG 1: SỐ TỰ NHIÊN (SỐ HỌC) |
1. Tập hợp. Phần tử của tập hợp.
- Người ta thường dùng các chữ cái in hoa A, B, C, .. để kí hiệu tập hợp. - Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, cách nhau bởi dấu chấm phẩy. Mỗi phần tử chỉ liệt kê một lần, thứ tự liệt kê tuỳ ý. - Kí hiệu: Phần tử x thuộc tập hợp A được kí hiệu là: \( x \in A \). Phần tử y không thuộc tập hợp A được kí hiệu là: \( y \not \in A \). - Để cho một tập hợp, thường có 2 cách: a) Liệt kê các phần tử của tập hợp. b) Chỉ ra các tính chất đặc trưng cho các phần tử của tập hợp.
2. Tập hợp số tự nhiên. Ghi số tự nhiên.
- Số tự nhiên bao gồm các số 0; 1; 2; 3; 4; ... - Tập hợp số tự nhiên kí hiệu là N: \( N = \{ 0; 1;2; 3; 4; 5; 6; ... \} \) - Tập hợp số tự nhiên khác 0 kí hiệu là \( N^* \): \( N^* = \{ 1;2; 3; 4; 5; 6; ... \} \) - Tính chất bắc cầu: nếu a < b và b < c thì a < c . - Ghi số tự nhiên: a) Ta dùng 10 chữ số 0, 1 ; 2 ; 3; 4; 5 ; 6; 7; 8; 9 để viết các số tự nhiên. b) Ngoài ra ta có thể dùng các chữ số La Mã để viết các số tự nhiên.
3. Các phép tính trong tập hợp số tự nhiên.
🍅 Phép cộng:
| a | + | b | = | c |
| số hạng | số hạng | tổng |
🍅 Phép trừ:
| a | - | b | = | c |
| số bị trừ | số trừ | hiệu |
🍅 Phép nhân:
| a | . | b | = | c |
| thừa số | thừa số | tích |
🍅 Phép chia hết:
| a | : | b | = | c |
| số bị chia | số chia | thương |
( điều kiện b ≠ 0 )
🍅 Tính chất của các phép toán trong tập hợp số tự nhiên:
+ Giao hoán:
\( a+b=b+a \)
\( a.b=b.a \)
+ Kết hợp:
\( a + b + c = ( a+ b) + c = a + ( b+ c ) \)
\( a . b . c = ( a.b) . c = a.(b.c) \)
+ Cộng với số 0: \( a + 0 = 0 + a = a \)
+ Nhân với số 1: \( a.1=1.a = a \)
+ Phân phối giữa phép nhân và phép cộng:
\( a.(b+c ) = a.b + a.c \)
\( a.( b-c ) = a.b - a. c \)
4. Luỹ thừa với số mũ tự nhiên.
a) Lũy thừa: lũy thừa bậc n của số a là tích của n thừa số a. Kí hiệu: \( a^n \) , n ≠ 0
\( a^n = \underset{n \: thừa \: số \: a }{\underbrace{a.a.a...a}}\)
b) Nhân hai lũy thừa cùng cơ số: khi nhân hai lũy thừa cùng cơ số ta giữ nguyên cơ số rồi cộng các số mũ với nhau.
\( a^m . a^n = a^{m +n} \)
c) Chia hai lũy thừa cùng cơ số: khi chia hai lũy thừa cùng cơ số ta giữ nguyên cơ số rồi trừ các số mũ với nhau.
\( a^m : a^n = a^{ m-n } \), ( a ≠ 0 , m ≥ n )
5. Thứ tự thực hiện các phép tính.
a) Đối với biểu thức không có dấu ngoặc: ta làm theo thứ tự sau Lũy thừa → Nhân, chia → Cộng, trừ b) Đối với biểu thức có dấu ngoặc: ta làm trong ngoặc trước, ưu tiên theo thứ tự sau Ngoặc tròn ( ) → Ngoặc vuông [ ] → Ngoặc nhọn { }
6. Chia hết và chia có dư. Tính chất chia hết của một tổng.
🌴 Chia hết, chia có dư: với a,b là 2 số tự nhiên + Nếu \( a = b.q , ( q \in N ) \) thì ta nói a chia hết cho b . + Nếu \( a = b.q + r , ( q, r \in N, 0< r < b ) \) thì ta nói a chia b dư r.
🌴 Tính chất chia hết của một tổng: \( a \: ⋮ \: m , b \: ⋮\: m ⇒ ( a ± b ) \: ⋮ \: m \) \( a ⋮ m , b \: \not \vdots m ⇒ ( a ± b )\: \not \vdots \: m \) Mở rộng tính chất: \( a \: ⋮ \: m , b \: ⋮ \: m, c \: ⋮\: m ⇒ ( a ± b ± c ) \: ⋮ \: m \) \( a \: ⋮ \: m , b \: ⋮ \: m, c \: \not \vdots \: m ⇒ ( a ± b ± c ) \: \not \vdots \: m \)
7. Dấu hiệu chia hết cho 2, cho 5.
🍄 Dấu hiệu chia hết cho 2: những số có chữ số tận cùng là 0; 2; 4; 6; 8 ( số chẵn ) thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2. 🍄 Dấu hiệu chia hết cho 5: những số có chữ số tận cùng là 0; 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
8. Dấu hiệu chia hết cho 3, cho 9.
🍎 Dấu hiệu chia hết cho 9: những số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9. 🍎 Dấu hiệu chia hết cho 3: những số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.
9. Ước và bội.
🐛 Ước và bội: nếu số tự nhiên a chia hết cho số tự nhiên b, ta gọi a là bội của b và b là ước của a. Kí hiệu: Ước của a, kí hiệu: Ư(a) Bội của a, kí hiệu: B(a) 🐛 Cách tìm ước: để tìm ước của số tự nhiên a ( a >1 ), ta lấy a chia lần lượt các số tự nhiên từ 1 đến a, a chia hết cho số nào thì số đó là ước của a. Ví dụ: Ư(6) = { 1;2;3;6 } 🐛 Cách tìm bội: để tìm bội của số tự nhiên a, ta lấy a nhân lần lượt cho các số tự nhiên 0; 1; 2; 3; 4; ... Ví dụ: B(3) = { 0; 3; 6 9; 12; ... }
10. Số nguyên tố. Hợp số. Phân tích một số ra thừa số nguyên tố.
🍛 Số nguyên tố. Hợp số. - Số nguyên tố: là số tự nhiên lớn hơn 1 và chỉ có 2 ước là 1 và chính nó. - Hợp số: là số tự nhiên lớn hơn 1 và có nhiều hơn 2 ước. 🍛 Phân tích một số ra thừa số nguyên tố: Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng tích các thừa số nguyên tố. - Ví dụ: \( 24 = 2.2.2.3 = 2^3.3 \)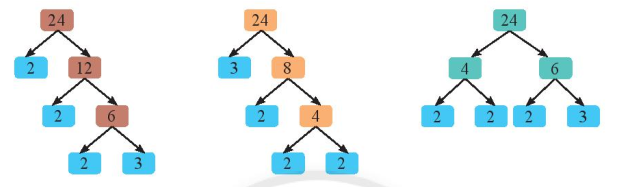
11. Ước chung. Ước chung lớn nhất.
🍨 Ước chung: ước chung của hai hay nhiều số là ước của tất cả các số đó. - Tập hợp ước chung của a và b kí hiệu: ƯC(a, b). - Nếu \( x \in ƯC(a,b) \) thì x ⋮ a , x ⋮ b. - Để tìm ƯC(a,b) ta tìm Ư(a), Ư(b) rồi chọn số chung của chúng. 🍨 Ước chung lớn nhất: ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp ước chung của các số đó. - Ước chung lớn nhất của a và b kí hiệu: ƯCLN(a,b). - ƯCLN(a,1) = 1.
🍨 Cách tìm ƯCLN bằng cách phân tích các số ra thừa số nguyên tố: Để tìm ƯCLN của hai hay nhiều số lớn hơn 1, ta làm các bước sau: + Bước 1: phân tích mỗi số ra thừa số nguyên tố. + Bước 2: chọn ra các thừa số nguyên tố chung. + Bước 3: lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.
12. Bội chung. Bội chung nhỏ nhất.
☕️ Bội chung: bội chung của hai hay nhiều số là bội của tất cả các số đó. - Bội chung của a và b, kí hiệu: BC (a,b). - Để tìm BC(a,b), ta tìm B(a) và B(b) sau đó chọn các số chung của chúng.
☕️ Bội chung nhỏ nhất: bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp bội chung của các số đó. - Bội chung nhỏ nhất của hai số a và b, kí hiệu: BCNN( a,b). - BCNN(a,1) = a.
☕️ Cách tìm BCNN bằng cách phân tích các số ra thừa số nguyên tố. Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta làm các bước sau: + Bước 1: Phân tích mỗi số ra thừa số nguyên tố. + Bước 2: Chọn ra các thừa số nguyên tố chung và riêng. + Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
| CHƯƠNG 2. SỐ NGUYÊN (SỐ HỌC) |
1. Số nguyên âm.
- Số nguyên âm được ghi lại như sau: -1; -2; -3; -4; ... và được đọc là: âm một, âm hai, âm ba; âm bốn, ... - Số nguyên âm được dùng để biểu diễn nhiệt độ dưới \( 0^0 C\), độ cao dưới mực nước biển, số tiền nợ, thời gian trước Công nguyên, ...
2. Tập hợp số nguyên.
- Tập hợp số nguyên bao gồm số nguyên âm, nguyên dương và số cả số 0. - Kí hiệu: \( Z \) Z = { ...; -3; -2; -1; 0; 1; 2; 3; ... }
3. Số đối của số nguyên.
- Số đối: hai số nguyên trên trục số nằm ở hai phía của điểm 0 và cách đều điểm 0 được gọi là hai số đối nhau. - Ví dụ: 6 là số đối của - 6 - 5 là số đối của 5 Số đối của 0 là 0.
4. So sánh hai số nguyên:
+ Số nguyên dương > 0. + Số nguyên âm < 0. + Số nguyên dương > số nguyên số âm + Trên trục số: Số lớn nằm bên tay phải của số nhỏ hơn.
5. Cộng hai số nguyên cùng dấu.
- Muốn cộng hai số nguyên dương, ta cộng như hai số tự nhiên. - Muốn cộng hai số nguyên âm, ta cộng hai số đối của chúng rồi thêm dấu trừ trước kết quả. - Tổng của hai số nguyên cùng dấu luôn cùng dấu với số nguyên đó. - Ví dụ: \( (+5) + (+7) = 5+7=12 \) \( (-5) + (-13) = - (5 + 13) = -18 \)
6. Cộng hai số nguyên khác dấu.
a) Cộng hai số nguyên đối nhau: tổng hai số nguyên đối nhau luôn bằng 0. \( a + (-a) = 0 \) b) Cộng hai số nguyên khác dấu không đối nhau: + Nếu số nguyên dương lớn hơn số đối của số nguyên âm, ta lấy số nguyên dương trừ cho số đối của số nguyên âm. + Nếu số nguyên dương bé hơn số đối của số nguyên âm, ta lấy số đối của số nguyên âm trừ cho số nguyên dương rồi thêm dấu trừ trước kết quả. + Ví dụ: \( 45 + ( -13) = 45 -13 = 32 \) \( 76 + ( -100) = - ( 100 - 76 ) = -24 \)
7. Tính chất của phép cộng số nguyên.
- Tính chất giao hoán: \( a + b = b + a \) - Tính chất kết hợp: \( ( a + b ) + c = a + ( b+ c ) \)
8. Phép trừ hai số nguyên.
- Muốn trừ số nguyên a cho số nguyên b, ta cộng số nguyên a với số đối của b. \( a - b = a + ( -b) \) - Ví dụ: a) \( 12 - 60 = 12 + ( -60 ) = - ( 60 -12 ) = - 48\) b) \( (-4) - (-13 ) = ( -4 ) + 13 = 13 - 4 = 9 \)
9. Quy tắc dấu ngoặc.
Quy tắc: - khi bỏ ngoặc trước ngoặc có dấu cộng "+" thì ta vẫn giữ nguyên dấu của các số hạng trong ngoặc. \( + ( a+b -c ) = a + b- c \) - khi bỏ ngoặc trước ngoặc có dấu trừ "-" thì ta đổi dấu của các số hạng trong ngoặc. \( - ( a+b -c ) = - a - b + c \)
10. Nhân hai số nguyên khác dấu.
a) Quy tắc: khi nhân hai số nguyên khác dấu, ta nhân số nguyên dương với số đối của số nguyên âm rồi b) Ví dụ: \( (-12). 5 = - ( 12. 5 ) = - 60 \) \( 21 . ( - 7 ) = - ( 21 . 7 ) = - 147 \)
11. Nhân hai số nguyên cùng dấu.
a) Quy tắc: - Khi nhân hai số nguyên cùng dương, ta nhân chúng như nhân hai số tự nhiên. - Khi nhân hai số nguyên cùng âm, ta nhân hai số đối của chúng. b) Ví dụ: \( ( +4). (+ 23 ) = 4. 23 = 72 \) \( ( -35) . ( -2 ) = 35 . 2 = 70 \)
12. Tính chất của phép nhân số nguyên.
- Tính chất giao hoán: \( a . b = b. a \) - Tính chất kết hợp: \( a ( b.c) = ( a.b ) . c \) - Tính chất phân phối của phép nhân đối với phép cộng ( hoặc trừ ): \( a. ( b+c) = a .b + a. c \) \( a. ( b - c) = a .b - a. c \)
13. Quan hệ chia hết và phép chia hết trong tập hợp số nguyên.
Cho \( a, b \in Z \) và \( b ≠ 0 \). Nếu có số nguyên q sao cho \( a = b.q \) thì: - Ta nói a chia hết cho b, kí hiệu là: \( a \: ⋮ \: b \). - Trong phép chia hết, dấu của thương hai số nguyên cũng giống như dấu của tích. ( + ) : ( + ) = ( + ) ( + ) : ( - ) = ( - ) ( - ) : ( + ) = ( - ) ( - ) : ( - ) = ( + ) Ta gọi q là thương của phép chia a cho b, kí hiệu là: \( a : b = q \)
14. Bội và ước của số nguyên.
Cho \( a, \: b \in Z \). Nếu \( a \: ⋮ \: b \) thì ta nói a là bội của b và b là ước của a.
| CHƯƠNG 3. CÁC HÌNH PHẲNG TRONG THỰC TIỄN (HÌNH HỌC) |
1. Hình vuông.
a) Hình vuông ABCD có: - Bốn đỉnh: A, B, C, D. - Bốn cạnh bằng nhau: AB = BC = CD = DA. - Bốn góc bằng nhau và bằng góc vuông. - Hai đường chéo là AC và BD. b) Cách vẽ hình vuông: dùng eke vẽ tứ giác có 4 cạnh bằng nhau và có bốn góc là góc vuông. 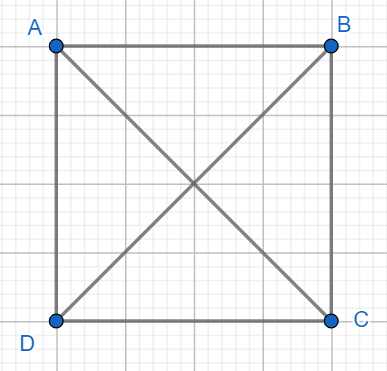
2. Tam giác đều.
a) Tam giác ABC có: - Ba đỉnh A, B, C. - Ba cạnh bằng nhau. - Ba góc bằng nhau. Tam giác ABC như thế được gọi là tam giác đều. b) Cách vẽ tam giác đều: dùng compa để vẽ tam giác có 3 cạnh bằng nhau.
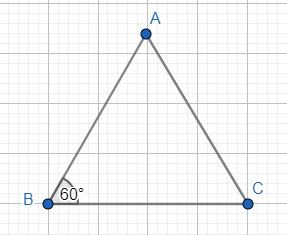
3. Lục giác đều.
Hình ABCDEF có: - Sáu đỉnh: A, B, C, D, E, F. - Sáu cạnh bằng nhau: AB = BC = CD = DE = EF = FA. - Sáu góc ở đỉnh A, B, C, D, E, F bằng nhau. - Ba đường chéo chính là: AD, BE, CF. Hình ABCDEF như thế được gọi là hình lục giác đều. 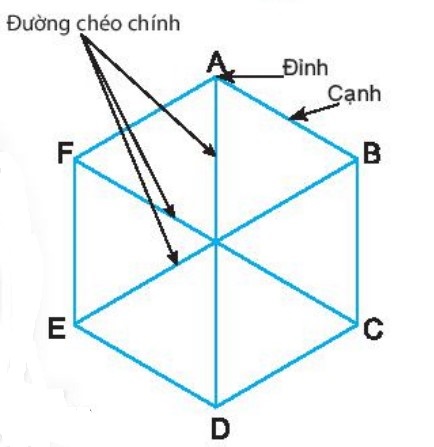
4. Hình chữ nhật.
Hình chữ nhật ABCD có: - Bốn đỉnh: A, B, C, D. - Hai cặp cạnh đối diện bằng nhau: AB = CD; BC = AD. - Hai cặp cạnh đối diện song song: AB song song với CD AD song song với BC - Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mổi đường. AC = BD; OA = OB = OC = OD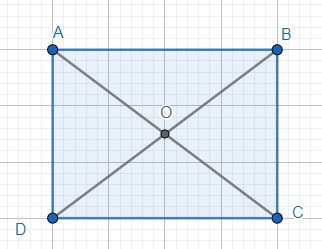
5. Hình thoi.
Hình thoi ABCD có: - Bốn đỉnh: A, B, C, D. - Bốn cạnh bằng nhau: AB = BC = CD = DA. - Hai cặp cạnh đối diện song song với nhau: AB song song với CD AD song song với BC - Hai đường chéo AC và BD vuông góc với nhau.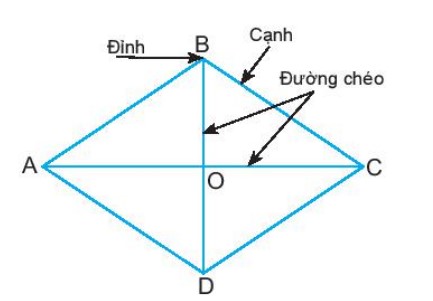
6. Hình bình hành.
Hình bình hành ABCD có: - Bốn đỉnh: A, B, C, D. - Hai cặp cạnh đối diện bằng nhau: AB = CD ; BC = AD. - Hai cặp cạnh đối diện song song: AB song song với CD BC song song với AD. - Hai cặp góc đối diện bằng nhau: góc A bằng góc C; góc B bằng góc D. - Hai đường chéo cắt nhau tại trung điểm của mổi đường: OA = OC OB = OD.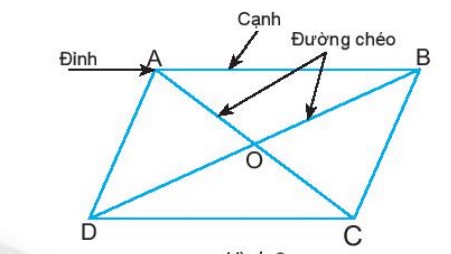
7. Hình thang cân.
Hình thang ABCD có: - Hai cạnh đáy song song: AB song song với CD. - Hai cạnh bên bằng nhau: AD = BC. - Hai góc kề một đáy bằng nhau: góc A bằng góc B, góc C bằng góc D. - Hai đường chéo bằng nhau: AC = BD. Hình thang ABCD như thế gọi là hình thang cân.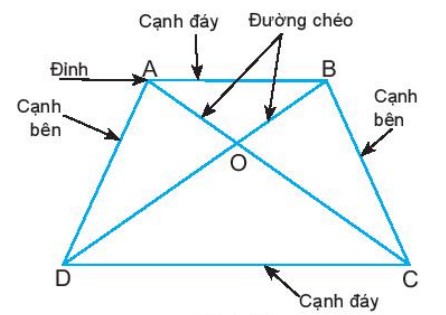
8. Chu vi và diện tích của một số hình.
9. Tính chu vi và diện tích một số hình trong thực tiễn.
| CHƯƠNG 4. MỘT SỐ YẾU TỐ THỐNG KÊ (THỐNG KÊ) |
1. Thu thập và phân loại dữ liệu.
2. Phân loại dữ liệu.
3. Tính hợp lí của dữ liệu.
4. Bảng dữ liệu ban đầu.
5. Bảng thống kê.
6. Biểu đồ tranh.
7. Biểu đồ cột - Biểu đồ cột kép.


