Bài 1: Điều tra về số lần tâng bóng của các “cầu thủ” lóp 7A tại một trường THCS. Thầy huấn luyện viên ghi nhận kết quả trong bảng sau:
| Số lần tân bóng (x) | 5 | 10 | 15 | 20 | 30 | |
| Tần số (n) | 3 | 5 | 10 | 8 | 6 | N = 32 |
a) Lớp 7A có bao nhiêu học sinh? Có bao nhiêu học sinh tâng bóng được nhiều nhất?
b) Vẽ biểu đồ đoạn thẳng.
Bài 2:
1) Cho đơn thức: \( A = \cfrac{ 3}{4 } x^3 y \left ( - \cfrac{1 }{ 3} xy^2 \right ) \)
a) Thu gọn và tìm bậc của đơn thức A.
b) Tính giá trị đơn thức A tại \( x = -2, y = 3 \).
2) Cho đa thức \( P(x) = x^4 -3x^2 -7 +4x^3 -x +4x^2 +9 -4x^3 + x \)
a) Thu gọn đa thức P(x) và sắp xếp các hạng tử theo lũy thừa giảm dần của biến; cho biết hệ số tự do, hệ số cao nhất.
b) Chứng tỏ đa thức P(x) không có nghiệm.
Bài 3:
1) Cho hai đa thức \( A = 3x^2 -7y^3 - 3x^2y^2\); \( B = 4 + 3x^2y^2 - 7y^3 \).
a) Tính A+B
b) Tính A - B
2) Tìm nghiệm đa thức: \( x^2 -16 \)
Bài 4: Cho tam giác ABC vuông tại A. Vẽ đường phân giác BD của \( \widehat{ ABC} ( D \in AC ) \).
1) Giả sử AB = 12cm; AD = 5cm. Tính độ dài đoạn thẳng BD.
2) Vẽ AE vuông góc với BD ( \( E \in BD) \) , tia AE cắt cạnh BC tại H ( \( H \in BC \) ) . Chứng minh: \( AB = HB \)
3) Chứng minh: DH vuông góc với BC
Bài 5: Cho hình vẽ, biết ΔDEF có \( \widehat{ E}= 58^0, \widehat{ F}= 40^0 \). Vẽ DH vuông góc với EF (\( H \in EF \) ).
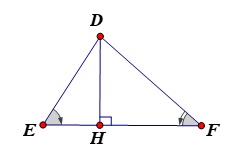
Chứng minh: \( EF < DH < HF \)
---------------- Hết --------------------


