Bài 1: Giải các phương trình sau:
a) \( 5(x^2 +1) -3x (x+3)n= 10 \)
b) \( 4x^4 + 11x^2 -20 = 0 \)
Bài 2:
a) Vẽ đồ thị hàm số \( (P): y = \cfrac{ }{ } x^2 \) trên mặt phẳng toạ độ.
b) Tìm toạ độ các giao điểm của (P) và đường thẳng \( (d): y = 2x + 6 \) bắng phép toán.
Bài 3:
Cho phương trình: \( x^2 -2mx + m^2 -2m + 4 = 0 \) ( m: tham số )
a) Tìm điều kiện của m để phương trình trên có nghiệm.
b) Tính tổng và tích hai nghiệm \( x_1; x_2 \) theo m.
c) Tìm các giá trị của m để hai nghiệm \( x_1; x_2 \) của phương trình thoả hệ thức: \( x_1^2 +x_2^2 - x_1 x_2 = 15 \)
Bài 4:
Để tổ chức tham quan hướng nghiệp cho 435 người gồm học sinh khối 9 và giáo viên phụ trách, nhà trường đã thuê 11 chiếc xe gồm hai loại: loại 30 chỗ và loại 45 chỗ ngồi ( không kễ tài xế ). Hỏi nhà trường thuê mỗi loại bao nhiêu xe? Biết rằng không có xe nào còn trống chỗ ngồi.
Bài 5: Tính khoảng cách giũa hai điểm B và C, biết rằng từ vị trí A ta đo được \( AB = 234m, AC =185m \) và \( \widehat{ BAC} =53^0 \).
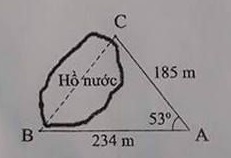
( Kết quả phép tính làm tròn đến hàng đơn vị )
Bài 6
Cho tam giác ABC có ba góc nhọn ( AB < AC ) nội tiếp đường tròn (O). Các đường cao AD, BE và CF của ΔABC cắt nhau tại H.
a) Chứng minh: các tứ giác BCEF và CDHE nội tiếp đường tròn.
b) Chứng minh: EH là phân giác của \( \widehat{ DEF} \) và \( EB.EH = ED.EF \).
c) Từ D kẻ một đường thẳng song song với EF cắt các đường thẳng AB, CF lần lượt tại M, N. Chứng minh D là trung điểm của MN.
-------------------------- Hết -----------------------------


