Bài 1: Giải phương trình:
a) \( 3x^2 -10x + 3 = 0 \)
b) \( 4x^4 + 5x^2 - 9 = 0 \)
Bài 2: Cho Parabol \( (P): y = \cfrac{ }{ } x^2 \) và đường thẳng \( (d): y = x+4 \)
a) Vẽ (P) và (d) trên cùng hệ trục toạ độ.
b) Tìm toạ độ giao điểm của (P) và (d) bằng phép tính.
Bài 3: Cho phương trình \( x^2 + (2m+1)x +m^2 - 3 = 0 \) ( m: tham số )
a) Tìm điều kiện của m để phương trình có nghiệm, rồi tính tổng tích các nghiệm theo m.
b) Giả sử \( x_1; x_2 \) là hai nghiệm của phương trình. Tính theo m giá trị của biểu thức:
\( A = x_1^2 +x_2^2 - x_1 x_2 \)
Bài 4: Một lớp học có 40 học sinh, trong đó nam nhiều hơn nữ. Trong giờ ra chơi, cô giáo đưa cả lớp 260.000đ để mỗi bạn nam một ly coca giá 5.000đ/ly, mỗi bạn nữ mua một bánh phô mai giá 8000đ/cái và được thối lại 3.000đ. Hỏi lớp có bao nhiêu học sinh nam, học sinh nữ?
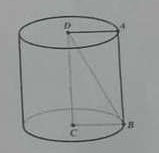
Bài 5: Cho hình trụ như hình bên. Cho \( BC = 15cm, DB = 25 cm \), tính thể tích hình trụ. ( \( \pi ≈ 3,14 \) )
Bài 6: Một cửa hàng piza bán hai loại bánh, loại 1 đường kính 40cm có giá 40.000đ và loại 2 đường kính 30cm có giá 30.000đ. Hỏi chọn mua loại nào có lợi hơn?
Bài 7: Từ điểm A ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là hai tiếp điểm ) và cát tuyến ADE ( D nằm giữa A và E, tia AE nằm giũa hai tia AB và AO ). Gọi I là trung điểm DE và H là giao điểm của AO và BC.
a) Chứng minh: tứ giác AIOC nội tiếp.
b) Chứng minh: \( AB^2 = AD.AE \) và \( \widehat{ EDO} = \widehat{ EHO} \)
c) Qua D kẽ đường thẳng song song với BE, đường thẳng này cắt AB, BC lần lượt tại M và N. Chứng minh \( MD= ND \).
-------------------- Hết -----------------------


