1. Tập hợp. Phần tử của tập hợp.
- Người ta thường dùng các chữ cái in hoa A, B, C, .. để kí hiệu tập hợp. - Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, cách nhau bởi dấu chấm phẩy. Mỗi phần tử chỉ liệt kê một lần, thứ tự liệt kê tuỳ ý. - Kí hiệu: Phần tử x thuộc tập hợp A được kí hiệu là: \( x \in A \). Phần tử y không thuộc tập hợp A được kí hiệu là: \( y \not \in A \). - Để cho một tập hợp, thường có 2 cách: a) Liệt kê các phần tử của tập hợp. b) Chỉ ra các tính chất đặc trưng cho các phần tử của tập hợp.
2. Tập hợp số tự nhiên. Ghi số tự nhiên.
- Số tự nhiên bao gồm các số 0; 1; 2; 3; 4; ... - Tập hợp số tự nhiên kí hiệu là N: \( N = \{ 0; 1;2; 3; 4; 5; 6; ... \} \) - Tập hợp số tự nhiên khác 0 kí hiệu là \( N^* \): \( N^* = \{ 1;2; 3; 4; 5; 6; ... \} \) - Tính chất bắc cầu: nếu a < b và b < c thì a < c . - Ghi số tự nhiên: a) Ta dùng 10 chữ số 0, 1 ; 2 ; 3; 4; 5 ; 6; 7; 8; 9 để viết các số tự nhiên. b) Ngoài ra ta có thể dùng các chữ số La Mã để viết các số tự nhiên.
3. Các phép tính trong tập hợp số tự nhiên.
🍅 Phép cộng:
| a | + | b | = | c |
| số hạng | số hạng | tổng |
🍅 Phép trừ:
| a | - | b | = | c |
| số bị trừ | số trừ | hiệu |
🍅 Phép nhân:
| a | . | b | = | c |
| thừa số | thừa số | tích |
🍅 Phép chia hết:
| a | : | b | = | c |
| số bị chia | số chia | thương |
( điều kiện b ≠ 0 )
🍅 Tính chất của các phép toán trong tập hợp số tự nhiên:
+ Giao hoán:
\( a+b=b+a \)
\( a.b=b.a \)
+ Kết hợp:
\( a + b + c = ( a+ b) + c = a + ( b+ c ) \)
\( a . b . c = ( a.b) . c = a.(b.c) \)
+ Cộng với số 0: \( a + 0 = 0 + a = a \)
+ Nhân với số 1: \( a.1=1.a = a \)
+ Phân phối giữa phép nhân và phép cộng:
\( a.(b+c ) = a.b + a.c \)
\( a.( b-c ) = a.b - a. c \)
4. Luỹ thừa với số mũ tự nhiên.
a) Lũy thừa: lũy thừa bậc n của số a là tích của n thừa số a. Kí hiệu: \( a^n \) , n ≠ 0
\( a^n = \underset{n \: thừa \: số \: a }{\underbrace{a.a.a...a}}\)
b) Nhân hai lũy thừa cùng cơ số: khi nhân hai lũy thừa cùng cơ số ta giữ nguyên cơ số rồi cộng các số mũ với nhau.
\( a^m . a^n = a^{m +n} \)
c) Chia hai lũy thừa cùng cơ số: khi chia hai lũy thừa cùng cơ số ta giữ nguyên cơ số rồi trừ các số mũ với nhau.
\( a^m : a^n = a^{ m-n } \), ( a ≠ 0 , m ≥ n )
5. Thứ tự thực hiện các phép tính.
a) Đối với biểu thức không có dấu ngoặc: ta làm theo thứ tự sau Lũy thừa → Nhân, chia → Cộng, trừ b) Đối với biểu thức có dấu ngoặc: ta làm trong ngoặc trước, ưu tiên theo thứ tự sau Ngoặc tròn ( ) → Ngoặc vuông [ ] → Ngoặc nhọn { }
6. Chia hết và chia có dư. Tính chất chia hết của một tổng.
🌴 Chia hết, chia có dư: với a,b là 2 số tự nhiên + Nếu \( a = b.q , ( q \in N ) \) thì ta nói a chia hết cho b . + Nếu \( a = b.q + r , ( q, r \in N, 0< r < b ) \) thì ta nói a chia b dư r.
🌴 Tính chất chia hết của một tổng: \( a \: ⋮ \: m , b \: ⋮\: m ⇒ ( a ± b ) \: ⋮ \: m \) \( a ⋮ m , b \: \not \vdots m ⇒ ( a ± b )\: \not \vdots \: m \) Mở rộng tính chất: \( a \: ⋮ \: m , b \: ⋮ \: m, c \: ⋮\: m ⇒ ( a ± b ± c ) \: ⋮ \: m \) \( a \: ⋮ \: m , b \: ⋮ \: m, c \: \not \vdots \: m ⇒ ( a ± b ± c ) \: \not \vdots \: m \)
7. Dấu hiệu chia hết cho 2, cho 5.
🍄 Dấu hiệu chia hết cho 2: những số có chữ số tận cùng là 0; 2; 4; 6; 8 ( số chẵn ) thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2. 🍄 Dấu hiệu chia hết cho 5: những số có chữ số tận cùng là 0; 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
8. Dấu hiệu chia hết cho 3, cho 9.
🍎 Dấu hiệu chia hết cho 9: những số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9. 🍎 Dấu hiệu chia hết cho 3: những số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.
9. Ước và bội.
🐛 Ước và bội: nếu số tự nhiên a chia hết cho số tự nhiên b, ta gọi a là bội của b và b là ước của a. Kí hiệu: Ước của a, kí hiệu: Ư(a) Bội của a, kí hiệu: B(a) 🐛 Cách tìm ước: để tìm ước của số tự nhiên a ( a >1 ), ta lấy a chia lần lượt các số tự nhiên từ 1 đến a, a chia hết cho số nào thì số đó là ước của a. Ví dụ: Ư(6) = { 1;2;3;6 } 🐛 Cách tìm bội: để tìm bội của số tự nhiên a, ta lấy a nhân lần lượt cho các số tự nhiên 0; 1; 2; 3; 4; ... Ví dụ: B(3) = { 0; 3; 6 9; 12; ... }
10. Số nguyên tố. Hợp số. Phân tích một số ra thừa số nguyên tố.
🍛 Số nguyên tố. Hợp số. - Số nguyên tố: là số tự nhiên lớn hơn 1 và chỉ có 2 ước là 1 và chính nó. - Hợp số: là số tự nhiên lớn hơn 1 và có nhiều hơn 2 ước. 🍛 Phân tích một số ra thừa số nguyên tố: Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng tích các thừa số nguyên tố. - Ví dụ: \( 24 = 2.2.2.3 = 2^3.3 \)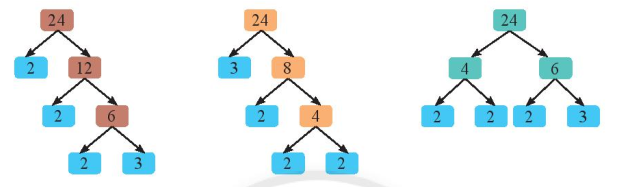
11. Ước chung. Ước chung lớn nhất.
🍨 Ước chung: ước chung của hai hay nhiều số là ước của tất cả các số đó. - Tập hợp ước chung của a và b kí hiệu: ƯC(a, b). - Nếu \( x \in ƯC(a,b) \) thì x ⋮ a , x ⋮ b. - Để tìm ƯC(a,b) ta tìm Ư(a), Ư(b) rồi chọn số chung của chúng. 🍨 Ước chung lớn nhất: ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp ước chung của các số đó. - Ước chung lớn nhất của a và b kí hiệu: ƯCLN(a,b). - ƯCLN(a,1) = 1.
🍨 Cách tìm ƯCLN bằng cách phân tích các số ra thừa số nguyên tố: Để tìm ƯCLN của hai hay nhiều số lớn hơn 1, ta làm các bước sau: + Bước 1: phân tích mỗi số ra thừa số nguyên tố. + Bước 2: chọn ra các thừa số nguyên tố chung. + Bước 3: lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.
12. Bội chung. Bội chung nhỏ nhất.
☕️ Bội chung: bội chung của hai hay nhiều số là bội của tất cả các số đó. - Bội chung của a và b, kí hiệu: BC (a,b). - Để tìm BC(a,b), ta tìm B(a) và B(b) sau đó chọn các số chung của chúng.
☕️ Bội chung nhỏ nhất: bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp bội chung của các số đó. - Bội chung nhỏ nhất của hai số a và b, kí hiệu: BCNN( a,b). - BCNN(a,1) = a.
☕️ Cách tìm BCNN bằng cách phân tích các số ra thừa số nguyên tố. Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta làm các bước sau: + Bước 1: Phân tích mỗi số ra thừa số nguyên tố. + Bước 2: Chọn ra các thừa số nguyên tố chung và riêng. + Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.


